What is Information Theory

Information theory is rooted in the work of Claude Shannon, who is one of the most influential scientists of the 20th century. He is considered to be the father of the digital age. In his landmark paper published in 1948, he developed an elegant theory called information theory, which introduced the modern concept of information and provided guidelines on how to efficiently acquire, compress, store and transmit information. Just as how Newton’s and Einstein’s theories shaped our understanding of the physical world, Shannon’s information theory has shaped our understanding of the digital world.

This fascinating video made by University of California Television explores Claude Shannon’s life and the major influence his work had on today’s digital world through interviews with his friends and colleagues.

Information Theory (Coding theorems)

For noiseless channels (source encoding)

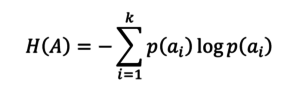
Assume that source of messages is given by its alphabet and by the probabilities of their appearances whereas a channel is given by its alphabet only. Then a limit of efficient compression is determined by such measure of source as its entropy

(This notion was introduced also by Shannon in terms of communication problems).

For noisy channels.

Let us consider a discrete noisy channel without memory (for simplicity) that can be given by full set of their symbol transition probabilities where x represents input symbols and are output symbols. Then there exists always (for simplicity) the main notion of this channel C, called a capacity by Shannon. Shannon’s theorem says that if the following condition holds

where Vs is the rate of source symbol generation and Vc is the rate of symbol transmission over the channel, then there is such encoding and decoding methods (they are some transformations of source sequences into channel sequences and vice versa), that the longer the length of these sequences the less the probability of decoding error. But if this inequality does not hold then such encoding and decoding procedures do not exist. In such a way due to a fair guess of Shannon it has been proved that under some conditions it is possible to get as good as desired reliability of information transmission over the noisy channels without a changing of channel parameters and information transmission rate!

It is worth noting that before 1948 most engineers believed that an improvement of information transmission reliability can be achieved only at the cost of either decreasing of information transmission rate (say multiple repetition of symbols) or at the cost of signal power increasing or channel band width increasing. A similar theorem has been formulated and proved by Shannon for continuous channels determined by their bandwidth and signal-to-noisy ratio and for continuous sources under the mean-square error criteria of source signal fidelity.

It is important to strike that Shannon’s theorems were theorems of existence that means that they establish strongly only a fact of good encoding and decoding presence but do not show how to find such procedures. The results established by Shannon are very actual also in present time. In fact, the price of power and frequency band is very high right now whereas the price of signal processing (say encoding and decoding) is going down due to a developing of micro chip technology and increasing of signal processor rates. The main results of Shannon have been presented for Russian readers in his monograph «Raboty po teorii informacii i kibernetike» translated in USSR by R.L Dobrushin and O.V.Lupanov under the edition of A.N.Kolmogorov (1963).

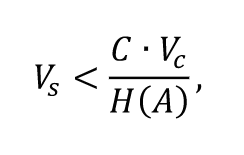
Information theory in Post-Shannon period

A more accurate description of coding theorem has been performed by Dobrushin, Pinsker, Fano, Wolfowitz, Solomon, Thomas-Cover and others. Calculation for the channel capacities for different channels was performed by Fink, Tsybakov, Fano, Gallager, and Csiszar. A finding of constructive encoding and decoding methods approaching the Shannon limit were undertaken by Slepian, Elias, Peterson, Gallager, Massey, Viterbi, Forney, Ziv, Sloan, Berger, Blahut, Verdu, Calderbank, Fink, Zigangirov, Zjablov, Gabidulin. The last achievements of coding theory led to

the fact that differences between energy gain predicted by Shannon and real energy gains for some channels differ only in parts of dB! (It is worth to note that in 60-70 years of the passed century the first two places among scientists in Information theory were occupied by American and Soviet ones.)

Below is a downloadable PowerPoint presentation presented by Michelle Effros and Vince Poor for the Shannon Centenary in 2016.

ShannonPDF